プロスペクト理論とは「ある事象が生じる確率や得られる損得が分かっている場合に、人間がどのような意思決定を行うかを理論化したもの」です。
行動心理学や経済学で非常に重要な理論ですが、学問的な言葉なので意味を理解するのが難しい言葉ですよね。
この記事では、理論の意味だけでなく、イメージを掴むための具体例も詳しく説明します。
☆「プロスペクト理論」をざっくり言うと……
| 読み方 | プロスペクト理論(ぷろすぺくとりろん) |
|---|---|
| 意味 | ある事象が生じる確率や得られる損得が分かっている場合に、人間がどのような意思決定を行うかを理論化したもの |
| 提唱者 | アメリカの心理学者であるダニエル・カールマンとエイモス・トベルスキー |
| 英語訳 | prospect theory |
このページの目次
「プロスペクト理論」の意味
ある事象が生じる確率や得られる損得が分かっている場合に、人間がどのような意思決定を行うかを理論化したもの
例:彼の不可解な行動は、プロスペクト理論で説明できる。
理論の概要
まずは理論の大まかな概要について説明します。
「プロスペクト理論」とは、ある事象が生じる確率や得られる損得が分かっている場合に、人間がどのような意思決定を行うかを理論化したものです。
「株取引やギャンブルなどの不確実な状況下で意思決定を行う際に、認識の歪みによって数値的な事実をそのまま受け取れない」ことを説明しています。
人間は、理屈としては合理的な意思決定がどれかわかっていても、感情などが邪魔をしてその判断ができないことが多いです。
このように、意思決定に客観的事実以外の、感情や置かれた状況が影響してしまうことを踏まえて、意思決定のようすをモデル化した理論がプロスペクト理論です。
具体的な内容
次に、プロスペクト理論の具体的な内容について説明します。
プロスペクト理論では、「意思決定の際に認識のゆがみが生じて、合理的な判断ができなくなること」が説明されています。
具体的に「認識のゆがみ」とは、何なのかを見ていきましょう。
プロスペクト理論を理解するうえで大切なのは、「人の意思決定は、目の前にある損失の度合いによって変化する」という考え方です。
人は「利益や得」と「損失」に異なる価値の重みを感じていると主張されています。
具体的に言えば、人は「利得を得て幸せなとき」よりも、「同等の損失による痛み」の方が大きく感じるのです。
「プロスペクト理論」の特徴

プロスペクト理論には、以下の3つの特徴が含まれています。
- 損失回避性(そんしつかいひせい)
- 参照点依存性(さんしょうてんいぞんせい)
- 感応度逓減性(かんのうどていげんせい)
それぞれの特徴を詳しく解説します。
特徴➀:損失回避性
損失回避性とは、「利益を追い求めるより、損失を避ける」という人間の心理的な傾向のことです。
人は100万円を手に入れる満足感よりも、100万円を失ったときの痛みの方に過剰に反応する傾向があります。
そのため、同じ程度の利益と損失があったときに、利益を追うよりも損失を避ける決断を下しがちです。
人は損失回避性が働くことで、以下のような心理状態に陥ります。
- 過剰に反応する
- 不必要に保守的になる
- 極度の恐怖心を抱く
特徴➁:参照点依存性
参照点依存性とは、「物事の主観的な価値は絶対的な価値にならない」と考える心理的傾向のことです。
具体的には、「物事の価値は参照点からの距離で決定する」とされる考え方です。
たとえば、オリンピックで二人の選手が以下のような結果が出たとします。
- 金メダルを確実視されていたが、銀メダルになったA選手
- メダルは困難といわれていたが、銅メダルを獲得したB選手
単純に順位やメダルの価値を考えた場合、A選手の銀メダルの方がB選手の銅メダルよりも価値が大きいはずです。
しかし、参照点依存性によって、人間はB選手の銅メダルのほうに高い価値を感じてしまうのです。
特徴➂:感応度逓減性
感応度逓減性とは「扱う金額が大きくなると、損得のインパクトが減少する」という心理現象のことです。
利益または損失の絶対値が大きくなるほど、変化への感覚が鈍ってしまうという心理の特徴を表します。
同じ1000円の変化だとしても、1万円が9000円になるのと、10万円が9万9000円になるのとでは、前者の方が大きな違いを感じると思います。
より具体的に例を挙げます。
スーパーで野菜を購入するときは10円の差額が重要に感じます。
その一方で、300万円の車を購入する場合には、5万円の差額を大きいものと感じないのです。
このように「あまりに高額な買い物をする場合、少額の誤差を簡単に受け入れてしまう」という心理傾向で感応度逓減性を感じることができます。
「プロスペクト理論」の二大柱

プロスペクト理論をより論理的に理解するためには、以下の2つの関数を知る必要があります。
- 価値関数
「価値の感じ方のゆがみ」を表すグラフ - 確率加重関数
「確率の感じ方のゆがみ」を表すグラフ
それぞれの関数について解説します。
関数➀:価値関数
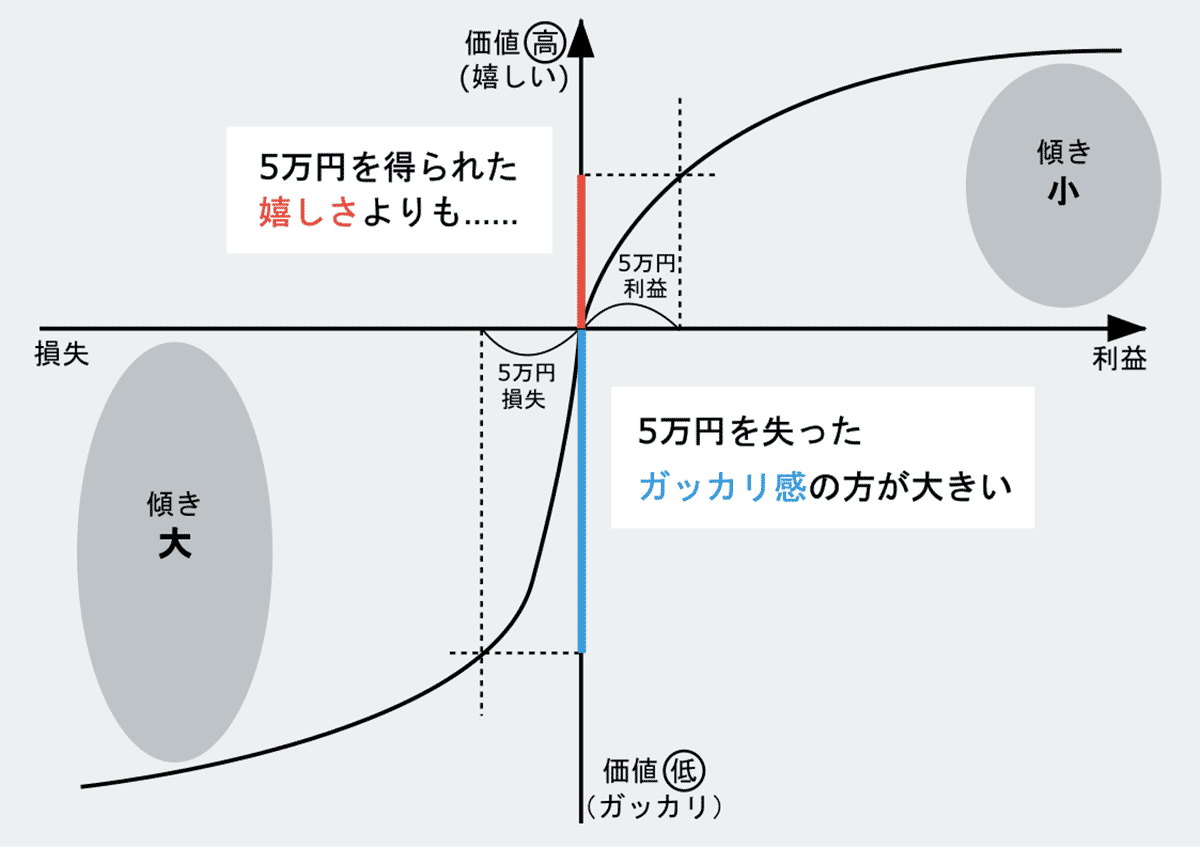
価値関数とは、私たちの認知における「価値の感じ方の歪み」を数値して表した関数です。
私たちには、「得をした嬉しさよりも、損をしたガッカリ感を強く感じる」という心理的な傾向があります。
たとえば、10万円を手に入れた時の喜びよりも、10万円を失ってしまったときのショックの方がより大きく感じられると感覚的にわかると思います。
経済学者の筒井義郎氏は、損失がもたらす影響は、利得のおよそ2.25倍だと結論付けています。
プロスペクト理論における価値観数を実際にグラフ化すると、以下のようになります。
 [出典:STUDY HACKER]
[出典:STUDY HACKER]
関数➁:確率加重関数
確率加重関数とは、私たちの「確率の感じ方のゆがみ」を表す関数です。
私たちは、客観的な数値である「確率」を完全に客観的に捉えることができません。
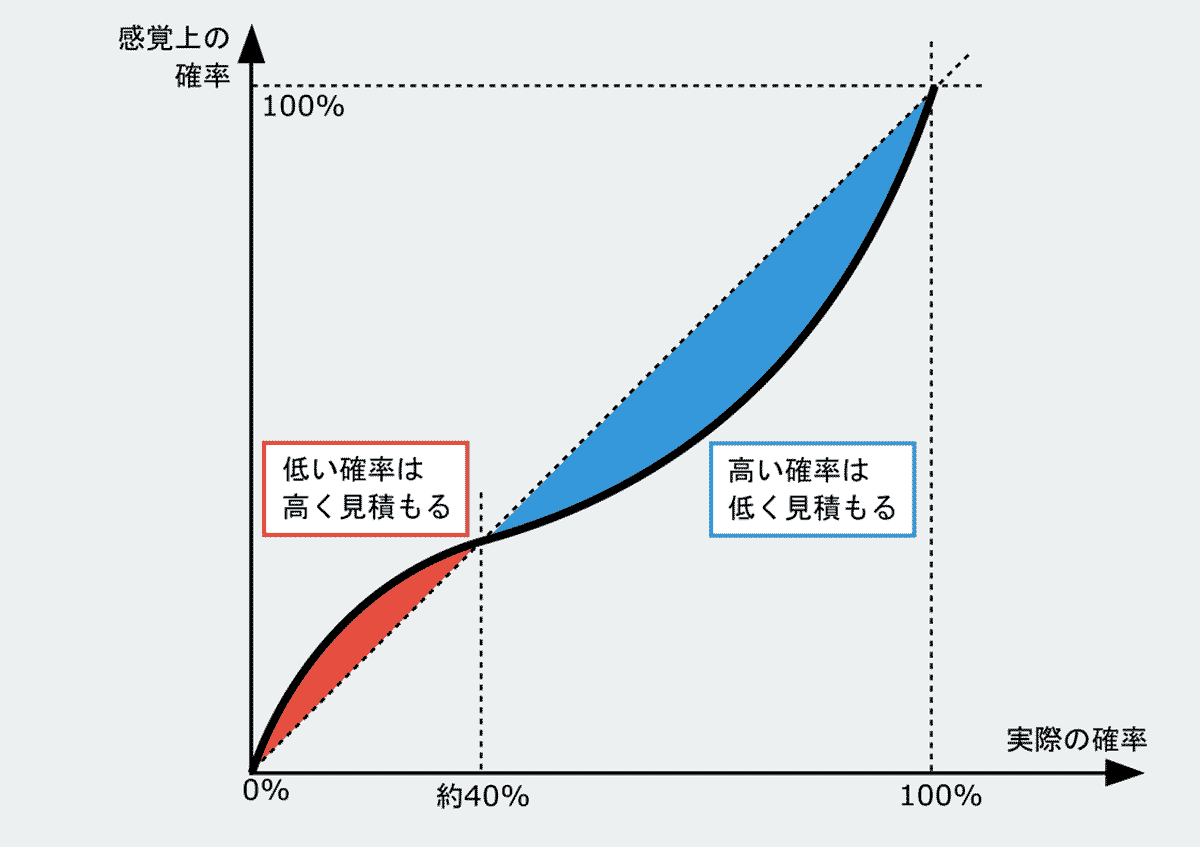
人間には「高い確率ほど低く見積もり、低い確率ほど高く見積もる」という心理的な傾向があるのです。
たとえば、0.00001%の確率で当たる宝くじは、限りなく当選確率が低いにも関わらず「意外と当たるんじゃないか」と考えてしまいます。
その一方で、高い確率は実際の数値よりも、感覚的には低く感じてしまいます。
たとえば、「手術の成功率は99%です」と言われても、「もしかすると失敗するかもしれない」と残りの1%が気になってしまうのです。
このような「確率の感じ方のゆがみ」を数値化して客観的に表したものが、確率加重関数です。
筒井義郎氏らは、確率加重関数において40%という値で確立の感じ方が切り替わると主張しています。
つまり、約40%以下の確率は実際の数値よりも高く感じられ、40%以上の確率は実際の数値よりも低く感じられるということです。
これらを踏まえて、確率加重関数をグラフ化すると以下のようになります。
 [出典:STUDY HACKER]
[出典:STUDY HACKER]
確率加重関数の40%というターニングポイントは、人によって異なります。
「プロスペクト理論」の具体例

プロスペクト理論を理解するための具体例を見ていきましょう。
プロスペクト理論を提唱する際の実験方法として使われた「一つだけの質問による心理学」という手法を例に挙げます。
例えば、次のような2つの選択肢があるときに、あなたならどちらを選ぶでしょうか。
- A:無条件で確実に100万円を受け取れる
- B:コインを投げて表が出たら200万円受け取れるが、裏が出たら何も受け取れない
AとBの条件の期待値は全く変わりません。
期待値とは、くじやギャンブルにおける「賞金額の平均」を表す値で、「報酬×確率」の式で求めることができます。
上記の2つの選択肢は、どちらも期待値が100です。
しかし、期待値が同じにも関わらず上記の条件の場合、ほとんどの人は「確実に100万円受け取れるAの選択肢を選ぶ」と言われています。
一方で、次の条件のときには、どちらの選択肢を選ぶでしょうか。
現在、200万円の借金を抱えているという前提の上で次の選択肢が提示されます。
- A:何もせずに100万円の借金が免除され、残りの借金は100万円となる
- B:コインを投げて表が出たら200万円の借金が全額免除されるが、裏が出たら1円も免除されない
この場合も2つの選択肢の期待値は、同様に100です。
しかし、この選択肢の場合、質問➀とは違い、多くの人がBの選択肢を選ぶと言われているのです。
このようにプラスとマイナスが入れ替わっただけにも関わらず、人の意思決定は大きく変化するのです。
意思決定が変化する理由
上記の具体例のように、意思決定が変わってしまうことを以下のように理由付けすることができます。
金額が2倍になっても価値は2倍にはならず、2倍弱になる
つまり人間は、受け取れる金額が2倍になったとしても、2倍嬉しいとは感じられないのです。
しかし、受け取れる確率が100%から50%に変化するのは非常に大きな変化だと感じられます。
このように考えると「2倍の金額を半分の確率で得る」というBの選択肢よりも、「1倍の金額を確実に得る」というAの選択肢の方が魅力的に感じられます。
日常的な「プロスペクト理論」の例
また、日常的には以下のような場面でプロスペクト理論が見られます。
- 恋愛
- FXや株式投資
- くじ
- 期間限定割引キャンペーン
- 全額返金キャンペーン
- ポイントサービスキャンペーン
例➀:恋愛
恋愛において、恋人がいるにも関わらず浮気をしてしまう人間の心理を、プロスペクト理論で以下のように説明できます。
- 浮気がばれる確率を低く見積もって浮気を続ける
- 損失を大きく感じる心理傾向によって、浮気相手を手放したくないと感じる
例➁:FXや株式投資
FXや株式投資は、プロスペクト理論がわかりやすく現れます。
人間は利益よりも損失を大きく感じるため、株価が下落すると損失に大きく反応し、なるべく損失が少ないうちに株を売却しようとする傾向があります。
逆に、利益に対しては損失よりも鈍感なので、株価が上昇してもすぐに利益を確定させることはしません。
例➂:くじ
人間はくじを引くときにプロスペクト理論によって、以下のような行動をとります。
- 当選金額は少なくても、必ず当たるくじを引く
利益を前にすると、確実に取れる利益を取ろうとする心理 - 損失のリスクは追いつつ当選確率を上げるためにくじをまとめ買いする
リスクを前にすると、リスクすべてを回避しようとする
➁では、「くじが外れる」というリスクをなくすためにくじをまとめ買いするという行動をとっています。
例➃:期間限定割引キャンペーン
商品やサービスの割引を常に行うのではなく、期間限定であることを強調して「期間中に得られる利益を確実に確保したい」と消費者に思わせる方法です。
購入までのリミットを設定することで、消費者が冷静な判断ができないように仕向けています。
例➄:全額返金キャンペーン
人間は、損失を大きく感じるという性質があります。
「もし商品が気に入らなかった場合には返品ができる」と言うことで損失を回避できるという安心感を消費者に与えます。
これによって、消費者が気軽に商品を購入できるようにしているのです。
例➅:ポイントサービスキャンペーン
人は、「得られるはずのものを得られない」よりも「すでに持っているものを失う」方が大きなショックを感じます。
そのため、有効期限付きのポイントをあらかじめ付与してしまうことで、「ポイントを失いたくない」という思いを起こさせて消費行動を促すのです。
「プロスペクト理論」の提唱者

プロスペクト理論の提唱者は、アメリカの心理学者であるダニエル・カールマンとエイモス・トベルスキーです。
1979年にプロスペクト理論が発表され、ダニエルカールマンは2002年にノーベル経済学賞を受賞しています。
プロスペクト理論が提唱されるまで、経済学やファイナンスといった学問の世界では「人間は合理的に行動する」ことが前提とされてきました。
しかし実際には、その前提をもとにすると説明できないような、投資家の非合理的な行動が多く存在していたのです。
そのような人間の非合理的な意思決定について説明した、画期的な理論がプロスペクト理論だったのです。
「プロスペクト理論」の類義語

プロスペクト理論には、以下のような類義語があります。
- 損失回避の法則
利益を追い求めるより、損失を避けるという心理的な傾向 - コンコルド効果
今まで投資してきたコストを惜しく感じてしまい、損失になるとわかっていても投資を継続してしまう心理 - フレーミング効果
物事の表現方法を変えることで、与える印象も変わること
「プロスペクト理論」と「フレーミング効果」の違い
フレーミング効果とは、同じ内容でも言い方や表現を少し変えることで、与える印象が大きく変わる現象を表します。
たとえば、以下のような言い換えがフレーミング効果を活用した表現です。
- 95%の確立で成功する手術
- 5%の確率で失敗する手術
手術の成功率は変わっていないのに、失敗する確率を前面に出されることで受ける印象が変わります。
これは、プロスペクト理論と同じく「利益より損失の回避を優先してしまう」という損失回避性を利用した印象操作のための理論です。
そしてプロスペクト理論は、損失回避性によって意思決定が変化してしまう現象そのものについて表す言葉なのです。
つまり、2つには以下のような違いがあるのです。
- プロスペクト理論
損失回避性を利用した印象操作のための理論 - フレーミング効果
損失回避性によって意思決定が変化してしまう現象そのもの
「プロスペクト理論」の英語訳

プロスペクト理論を英語に訳すと、次のような表現になります。
- prospect theory
(プロスペクト理論)
プロスペクト理論の語源は英語の “prospect” です。
“prospect” は、「予想、見通し、期待、展望」などと訳されます。
つまり「先を見据える」といったニュアンスの意味を持つ英単語なのです。
「プロスペクト理論」のまとめ
以上、この記事ではプロスペクト理論について解説しました。
| 読み方 | プロスペクト理論(ぷろすぺくとりろん) |
|---|---|
| 意味 | ある事象が生じる確率や得られる損得が分かっている場合に、人間がどのような意思決定を行うかを理論化したもの |
| 提唱者 | アメリカの心理学者であるダニエル・カールマンとエイモス・トベルスキー |
| 英語訳 | prospect theory |
非常に難しい言葉でしたが、この理論を理解しておけば合理的な判断ができるかもしれません。
この機会に覚えておきましょう。











